真有效值RMS如何准确测量

RMS即真有效值，是对交流信号幅度的基本量度，可以分别从实用角度和数学角度予以定义。

从实用角度定义是：一个交流信号的真有效值等于在同一电阻性负载上产生同等热量所需的直流量。例如，1V真有效值交流信号与1V直流信号在同一电阻上产生的热量相同。

从数学角度定义是：真有效值定义如下：

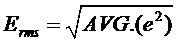
真有效值等同于零平均值统计信号的标准偏差。这包括求信号的平方，取平均值，然后获得其平方根。取平均的时间和信号的特性相关，对于周期信号，则使用完整周期进行平均即可，但是对于非周期信号，取平均值的时间必须足够长，以便能在所需的近似最低工作频率进行滤波。

按照RMS的定义，一个交流信号的RMS值等于在同一电阻性负载上产生同等热量所需的直流量。所以真有效值是从热量角度定义的，根据热量的定义，有以下公式：

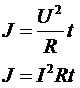
所以根据RMS定义，有以下公式：

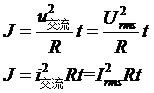
消去R值，可以得到

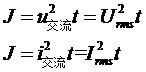
两个等式的模型一样，等效为一个等式：

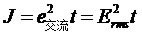
交流信号的幅度值是时刻变化的，但是我们将时间t细分为Δt，由于Δt很小，可以认为在Δt时间内交流信号的幅度值不变化，值为e(i)，并且热量是可以累积的，所以有：

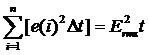
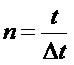
所以有：

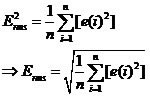
推导得到真有效值的数学定义，等效于对被测信号的实时采样值进行平方和后求平均，然后开方。求平均是一个将变化信号趋于稳定的运算，对于周期信号，因为其周期变化，所以只要对其完整周期进行评价，其结果就是一个稳定值，所以平均的时间t可以取周期信号的n个完整周期T。对于非周期信号，由于其变化没有规律，所以只能在保证测量结果输出的前提条件下，尽可能长时间的进行平均。

对于周期信号，当Δt无穷小时，我们可以得到RMS值得积分表达形式：

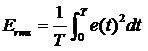
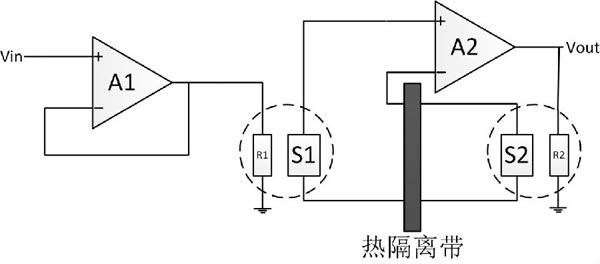
理论上，热转换是最简单、最直接的方法，但实际上，它却是最难以实现、成本最高的方法。这种方法涉及到将未知交流信号的热值与已知的校准直流基准电压的热值进行比较，测量框图如图1所示。基准电阻R2和信号电阻R1的等效参数模型必须是近似完全一致，并且近似纯电阻性。S1和S2是两个性能完全一样的热电转换器件，将R1和R2产生的热量转换为电形式，热隔离带用来阻断R1和R2之间的热传递，所以最终A2会调整一个直流输出值，使基准电阻R2与信号电阻R1之间的温差为零，此时这两个匹配电阻的功耗完全相同。因此，根据真有效值的基本定义，直流基准电压值将等于未知信号电压的真有效值。

模型非常简单，也非常好理解，但是每个热单元都必须含有一个稳定的、低温度系数电阻R1和R2，电阻与线性温度电压转换器S1和S2发生热接触，并且要保证热传递性能一致。

图1所示的电路框图对器件和系统有着严格的要求，但是通常也具有较小的误差和宽带宽的优点。但是，热转换单元R1和 S1、R2和S2具有一定，且固定的时间常数，所以对于过低频率的信号，需要较长时间才能稳定，并且温度波动会较大，所以了这种真有效值计算方案的低频性能不好。

显式计算就是按照真有效值的数学定义进行每一步运算。真有效值除了热量角度的定义外，还有一个数学定义，包括求信号的平方、取平均值、获得其平方根，显而易见，显示计算是利用乘法器和运算放大器直接进行平方、平均值和平方根计算。平方可以使用乘法器完成，平均可以使用低通滤波器完成，开方可以使用运放和乘法器完成。

显式计算法框图如图2所示，因为是连续的模拟测量，所以选择性能优秀的乘法器和运放可以实现相对不错的精度和带宽。但是因为经过平方器后的信号振幅范围会变得更大，为保证后级电路能够进一步处理，必须限制信号的动态范围，因此显式计算方法的动态范围有限。例如，如果输入信号的动态变化范围为20dB（1V至10V的输入），那么平方器输出信号的动态范围将达到40dB（平方器输出=1V至100V）。因此这类方法如果是单级运算则输入动态范围最大约为10:1，则最大可以实现20dB的动态范围。

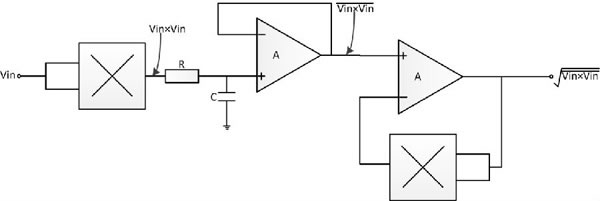
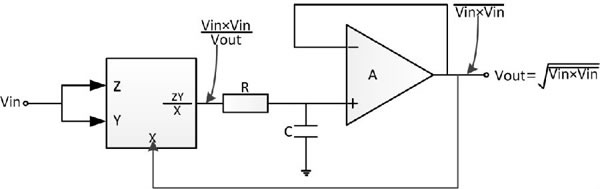
另外一种更好的计算方案是利用反馈在电路输入处隐式或间接地进行求平方根计算，如图3所示。平均值信号除以输出的平均值后，将与输入的真有效值呈线性变化，而非平方关系。与显式真有效值电路相比，这种隐式电路明显扩大了输入的动态范围。隐式计算的公式如下：

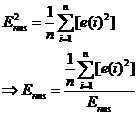
隐式真有效值计算与其它方法相比具有器件较少、动态范围较大、成本通常较低的优点。它的缺点是带宽一般比热真有效值计算或显式计算法要窄。隐式计算方案可以使用直接乘法和除法，或者使用一种对数-反对数电路技术。

模拟测量可以连续进行测量，给出测量结果，但是一般带宽和精度相对较低，因为其使用了低通滤波器进行平均运算，如果实现测量结果稳定，则必须使用极低的截止频率，而截止频率低这会导致测量速度非常慢。

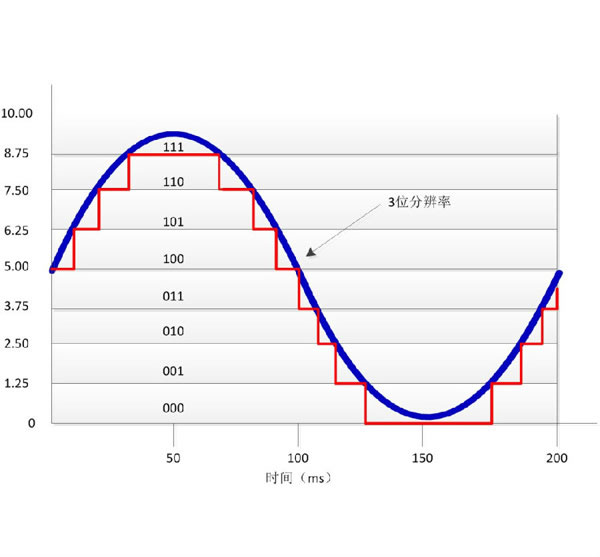
一种更高精度、更高带宽、更快速度的测试方法就是使用数字方法进行测量。数字测量使用前面推导的数字定义的公式，将模拟信号离散化，离散过程就是ADC对模拟信号采样的过程，如图4所示示意了一个3位分辨率的ADC对正弦信号离散化的过程。当采样率远远高于被测信号的频率时，即ADC的两个采样结果之间的时间间隔Δt非常短，这时我们可以近似认为在Δt时间内被测信号的值没有变化，就是ADC的采样值。然后我们利用真有效值的数学定义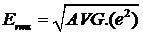进行运算即可得出真有效值。对于周期信号，我们可以使用一个或者多种周期进行运算，对于没有明显周期的信号，我们可以规定一定时间计算一次真有效值。

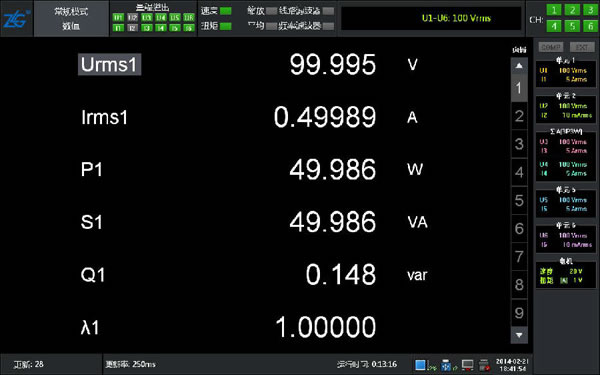
PA6000功率分析仪使用的就是这种数字方法实现真有效值的测量，测量周期由同步源决定，具体如何决定将在同步源知识点讲解。PA6000使用了数字方法测量，所以可以达到很高的带宽和精度，带宽高达1MHz，精度高达0.02%，这种精度和带宽是模拟测量无法实现的，同时最大支持10ms给出一个测量结果的速度也是模拟测量技术无法企及的一个速度。

常规的测量仪器无法准确测量出真有效值的原因是他们一般仅仅针对工频设计，带宽不够无法满足实际的测试需求，因为实际情况下电压和电流都可能含有丰富的谐波成分，而这些常规仪器的带宽往往不够，所以无法准确测量到高次谐波的能量，但是高次谐波却一样会导致电路元件发热，并且会导致容性元件急剧发热，实际中绝大多数电路元器件的极限容量值是由保证元器件不过热而可以散发的热量所决定的。

例如电缆的容量是由特定的安装条件和最大的工作温度所决定的。如果测量不准确会导致电缆的实际运行电流值被低估，因而导致电缆的工作温度比预期的温度要高，结果是电缆的绝缘下降、过早损坏甚至引发火灾。

其他的一些电力元器件，如熔断器和断路器的热元件，它们的额定电流值是根据有效值来制定的，因为它们的特性和散热紧密相关。这就是误跳闸的根本原因所在。真实电流大于所预期电流，导致断路器一直工作在过电流状态，长期工作可能会引起跳闸。任何由误跳闸引起的断电所造成的事故损失都可能是巨大的。

想了解更多功率分析仪信息，请点击/PA/ 。